The universe shouldn’t be here. Everything scientists know about particle physics, summed up in a theory called the Standard Model, suggests that the big bang should have created equal quantities of matter and antimatter. A mirror version of matter, antimatter consists of partner particles for all the regular particles we know of, equal in every way but with opposite charge. When matter and antimatter particles collide, they destroy one another, so the mass created when the universe was born should have been completely wiped out, leaving an empty, featureless cosmos containing only light. That there was enough leftover matter after this great annihilation to form galaxies, stars, planets and even us but almost no antimatter is known as the matter-antimatter imbalance. This existential anomaly is one of the great outstanding mysteries of modern physics.
Physicists have concocted many hypotheses to explain this mismatch, but we don’t know which, if any, are true. Some of them seek to offer matter the upper hand by introducing new particles that decay, producing more matter than antimatter in the process, or that interact differently with matter and antimatter. And some of these proposals include side effects that scientists can hope to detect, thereby providing evidence for the theories. One example is an exotic property of electrons called the electric dipole moment, a small difference between the center of mass of an electron and its center of charge. Such a displacement has never been detected and should be much smaller than current experiments could measure. But many proposed extensions to the Standard Model that seek to explain the matter-antimatter imbalance predict much larger values for the electric dipole moment.
Recently I worked with colleagues to attempt to detect this signal. Our laboratory, nestled against the foothills of the Rocky Mountains at JILA, a research institute of the University of Colorado Boulder, took a different route than usual experiments. We pioneered a new strategy that allowed us to make the most precise measurement yet of the electric dipole moment.
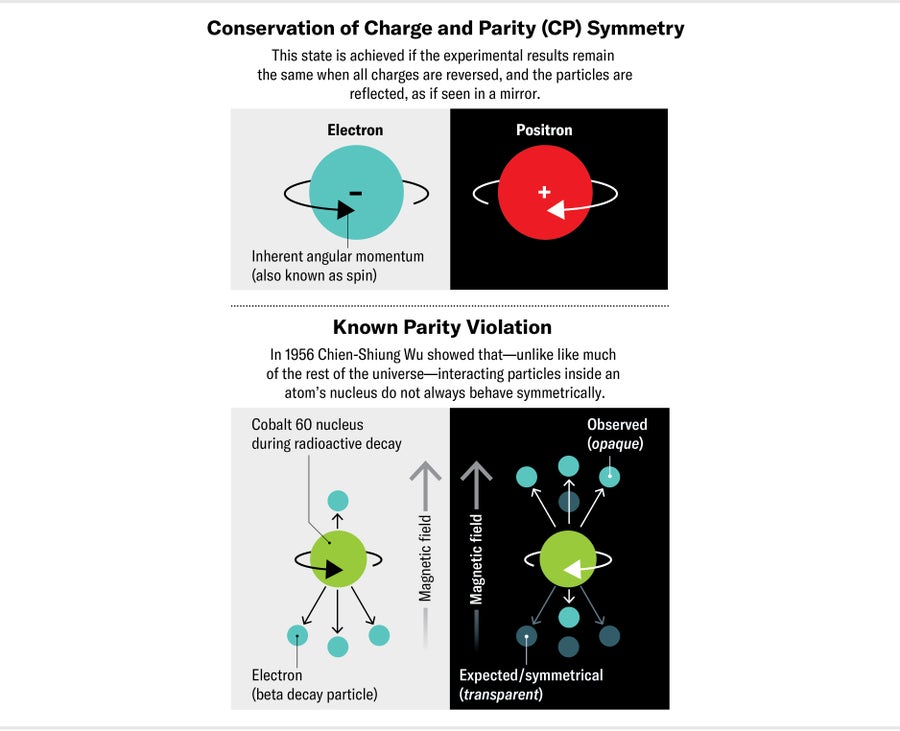
To understand what we were looking for, imagine any simple physics experiment. Now picture repeating that experiment with all positive charges replaced by negative ones (and vice versa) and the entire apparatus arranged in the opposite direction as if reflected in a mirror. If you got an equivalent result with the mirror setup, the experiment would be said to conserve charge and parity symmetry (CP symmetry for short). In 1967 physicist Andrei Sakharov showed that this symmetry is intimately connected to the matter-antimatter imbalance. If our universe as we currently find it developed from a universe that was initially composed of equal parts matter and antimatter, something must have happened to break CP symmetry, Sakharov found. Around the same time, other researchers discovered that nature does sometimes violate CP symmetry. For instance, the weak force—responsible for radioactivity in atomic nuclei—slightly breaks this symmetry when it interacts with quarks. Yet the instances of known CP violation in the Standard Model aren’t enough to explain the matter-antimatter imbalance. We must find new, undiscovered physics phenomena that don’t conserve CP symmetry to solve the mystery.
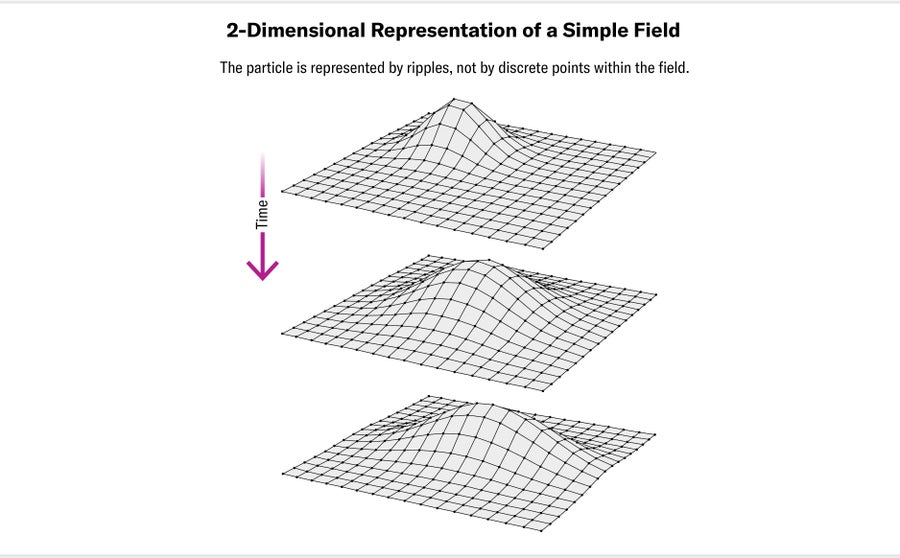
That’s where our experiment comes in. It searches for evidence of new particles in the universe by looking for subtle effects on known particles. These effects occur because of the nature of the Standard Model, which is a type of quantum field theory. In quantum field theories, the basic building blocks of the universe are fields, not particles. There is a field for each of the particles in nature, from common particles such as electrons and photons to their more exotic cousins such as muons and gluons. You can imagine two-dimensional analogues of these fields as huge, flexible sheets that extend through all of space, supporting ripples like the surface of a lake does. In a quantum field, ripples can occur only in certain discrete sizes. The smallest possible ripple in a given field is what we call a particle; positive ripples in the field are matter particles, and negative ripples in the field are antimatter particles.
The amount of energy it takes to create the smallest possible ripple depends on the stiffness of the stretchy sheet; this minimum amount of energy is the rest mass of the associated particle. The different fields are linked together—or “coupled”—so that a ripple in one field disturbs the connected fields. For example, an oscillating ripple in the electron field creates accompanying ripples in the electromagnetic field corresponding to photons, a phenomenon we make good use of in everyday devices such as radio antennae and mobile phones.
Physicists’ most successful tools for discovering new fields, and the particles associated with them, have historically been particle colliders. These machines direct two particles—protons, for example—to fly toward each other at high speeds. When the particles (ripples) crash into each other like two water waves meeting on a beach, their violent interactions can cause some of their energy to be carried off as ripples in other fields. If the energy of their collision is exactly equal to the energy needed to create a ripple in one of the other fields they are coupled to, we get what’s called resonant enhancement, which greatly increases the probability of a new particle being created. Such collision resonances were used to discover many of the fields we know about—including the most recently confirmed piece of the Standard Model, the Higgs field, with its associated particle, the Higgs boson.
The world’s most powerful accelerator, the 27-kilometer ring of the Large Hadron Collider (LHC) near Geneva, is now operating at the highest collision energies it was designed for, but so far it hasn’t discovered any other new fields. If undiscovered fields exist, either their mass is higher than the LHC can reach or their coupling to the fields of the Standard Model is too weak for the LHC to create them. A new particle collider capable of reaching much higher energies is likely to cost many tens of billions of dollars, and as a result, even agreeing on whether and how it should be funded is likely to take many years.
Luckily, there is another way to detect new particles and fields, which involves making precision measurements. As mentioned earlier, because the fields of the Standard Model are coupled, a ripple corresponding to a particle in one field always causes disturbances in other fields. For example, an electron—a ripple in the electron field—disturbs the electromagnetic field around it. This disturbance in the electromagnetic field in turn disturbs the other fields that are coupled to it, and so on, eventually including all known fields of the Standard Model. What we call an electron is actually a composite excitation of all these fields, like a large water wave causing disturbances in the air above it. The effect is sometimes referred to as the electron being surrounded by a cloud of “virtual particles.”
These accompanying disturbances of the other fields affect many of the electron’s properties, so by carefully measuring these properties, we can infer the presence of any undiscovered fields that are coupled to the electron. If those fields are associated with heavier particles, they are stiffer and therefore less disturbed by the rippling electron field—meaning they cause less of a change to the electron’s properties. Measuring the effects of fields with particles of higher and higher masses thus requires measurements with greater and greater precision.
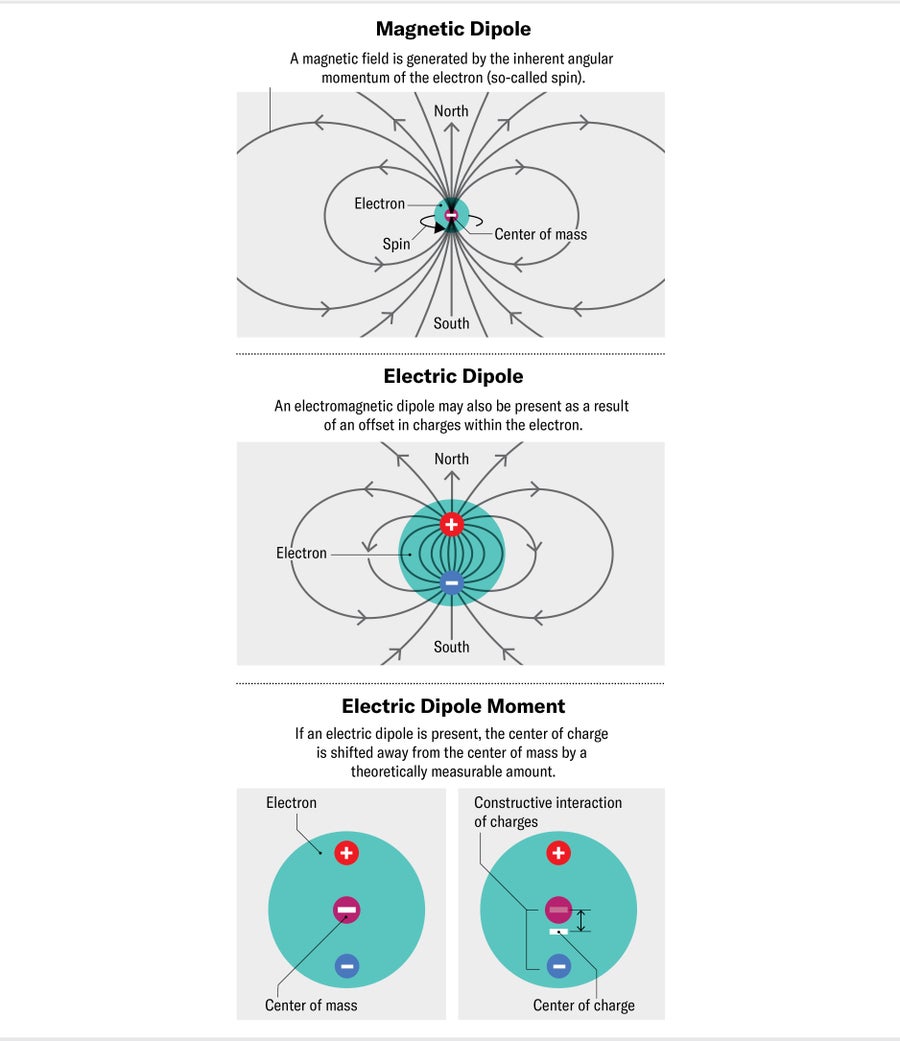
One difficulty of this approach is that often the kind of change we’re looking for is overshadowed by modifications from fields of the Standard Model. For example, an electron has a magnetic field similar to a tiny bar magnet. The strength of this field is the electron’s magnetic dipole moment, and it has been measured to very high precision. Its value is determined mostly by the magnetic moment of the bare electron field; the largest changes arise from the electromagnetic field, and they can be calculated with astonishing precision. At the level of precision achieved by current experiments, however, the exact value of the Standard Model coupling between an electron and electromagnetic fields is not exactly known—there is some discrepancy in the measured values from different experiments. Even if this problem is resolved, the tiny effects of interactions with quark fields and the strong force will be important. These effects can be incredibly complex and difficult to calculate, making our search for similar-sized (or smaller) effects from exotic physics challenging.
A nice way around this problem is to find a property that is zero (or very, very small) in the Standard Model. According to the theory, there should be only a minuscule separation between an electron’s center of mass and center of charge—in other words, its electric dipole moment. The electric dipole moment of an electron (eEDM), the electric counterpart of the magnetic moment, can essentially be caused only by interactions that violate CP symmetry. The CP violation contained within the Standard Model is exceedingly small, well below current experimental sensitivity. In contrast, many extensions to the Standard Model, proposed to help explain the matter-antimatter imbalance, predict eEDMs many orders of magnitude larger and within reach of near-term experiments.
I remember being extremely excited reading about these ideas for the first time as a physics student. In contrast to the enormous infrastructure and huge collaborations involved in running particle colliders like the LHC, experiments to measure everyday particles such as an electron can often fit on a (admittedly large) table in a conventional university laboratory and be handled by a few scientists. It was surprising to me that, in certain cases, these tests can answer questions about fundamental physics that the world’s most expensive experiments cannot. The tabletop projects also seemed much better suited to my personality. In large collaborations, individual roles are usually highly specialized; in contrast, running a tabletop experiment requires everyone to take a holistic view of the entire apparatus. We must be generalists, garnering passable knowledge of many different disciplines and technologies, from electronics and computer programming to lasers and vacuum chambers. I love this kind of variety and the chance to do something big with something relatively small.
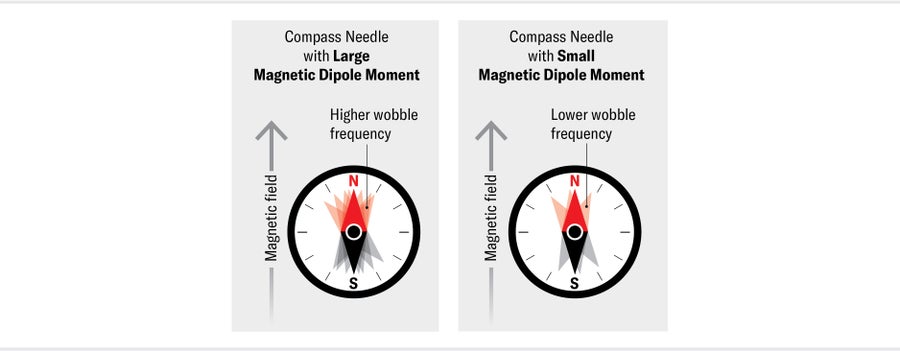
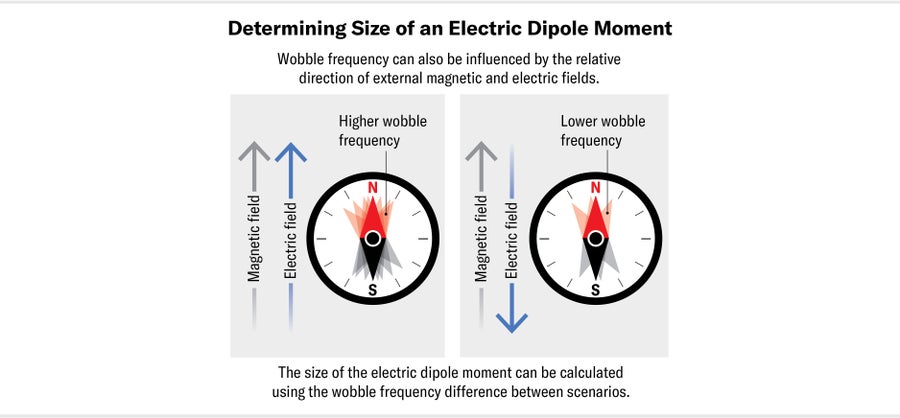
To say an electron has a nonzero electric dipole moment is equivalent to saying it has a preferred orientation in an electric field—just as the needle of a compass (which has a magnetic dipole moment) has a preferred orientation in Earth’s magnetic field. If a compass needle is briefly nudged, it will wobble backward and forward around magnetic north. The frequency of this wobble is proportional to both the strength of the magnetic field and the size of the magnetic dipole moment of the needle.
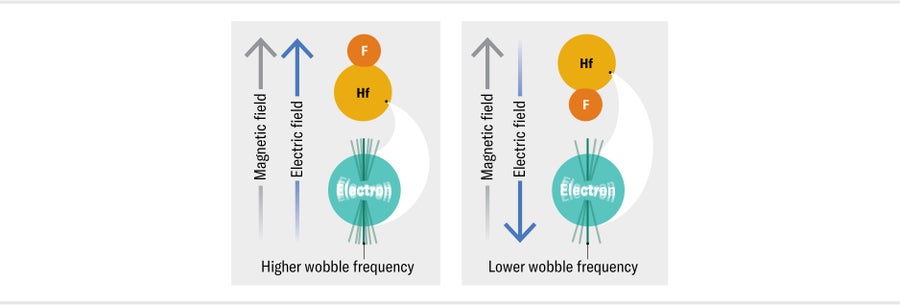
As a result, if you measure the frequency of the wobble in a known magnetic field, you will know the size of the needle’s magnetic dipole moment. If the needle also has an EDM, perhaps because we charged up one end of it somehow, we can measure its size by simultaneously applying an electric field. When the electric field is parallel with the magnetic field, the needle will wobble with a slightly increased frequency; when the electric field is pointing in the opposite direction, the wobble frequency will decrease. The difference between these two frequencies tells us the size of the needle’s EDM. We can search for the electron’s EDM in precisely the same way, first placing the particle in a magnetic field and then measuring the shift in its wobble frequency when we apply an electric field parallel and then antiparallel to that magnetic field.
We know the eEDM must be very tiny, if it exists at all, so we know we are looking for an extremely tiny shift in the wobble frequency. We can boost the signal by applying a larger electric field. A powerful way to do this is to use electrons confined inside heavy atoms and molecules. You might think that an electron in an atom or molecule wouldn’t experience any electric field, or else it would fly away. This is true, however, only if you ignore Einstein’s special theory of relativity. When relativity is taken into account, it turns out that in heavy atoms, where relativistic effects are most important because electrons move at close to the speed of light near the highly charged nucleus, the effective electric fields acting on the electron can be tremendous—around a million times larger than the strongest fields we can generate in a lab. To take advantage of this fantastically large field for our measurement, we need apply only enough of an electric field in the lab to orient the atom or molecule. This work turns out to be much easier with molecules, so for the past decade or so all the leading experiments of this type have used electrons in heavy molecules made of two atoms. Our experiment uses hafnium monofluoride molecules because hafnium, with 72 protons in its nucleus, is one of the heaviest metals in the periodic table that isn’t radioactive.
Even with this enormous electric field, the change in the wobble frequency of the electron that we might expect from a realistically sized EDM is still very tiny, corresponding to about one extra wobble every seven hours or so. To detect such a minuscule change, we need to measure the two frequencies, with the electric field parallel and then opposite to the direction of the magnetic field, extremely precisely. The longer we monitor a frequency, the more wobbles we can measure and therefore the more precise we can make our measurement.
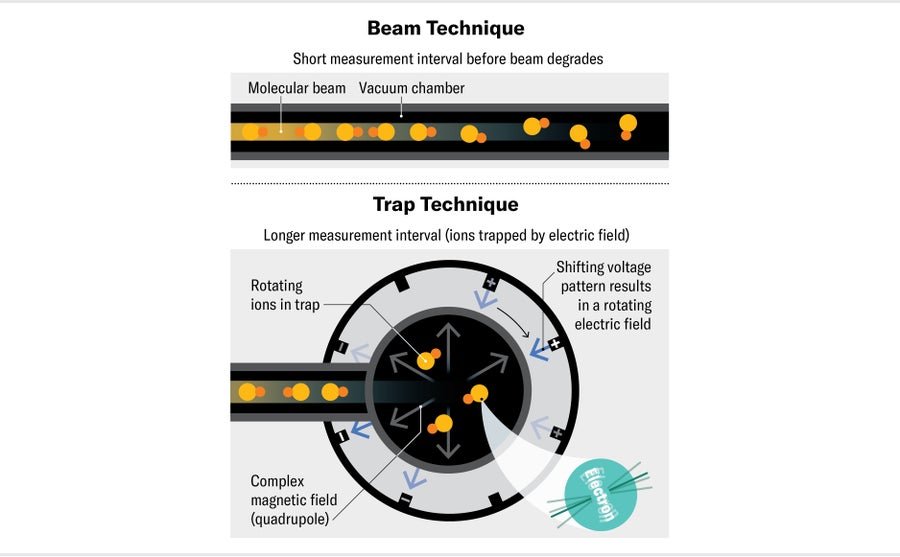
Our timing is limited by how long our molecules last. For these kinds of experiments, we must use molecules that have free, unpaired electrons, which makes them highly reactive—the electrons are eager to bond with any other atoms they encounter. We have to keep our molecules in vacuum chambers where they don’t come into contact with other particles or the walls of the chamber. Previous experiments have used beams of molecules traveling at hundreds of meters per second down a long vacuum chamber, with researchers observing the molecules in free flight. In this setup, the measurement time is limited by how long the beam of molecules can travel before it starts spreading out too much and the signal is lost. Typically this happens within about a meter, or around one millisecond.
For our experiment, we wanted to be able to observe the electrons for longer. We decided to use trapped molecular ions—charged molecules—which we held in position with electric fields. Trapping molecular ions this way isn’t new, but no one had previously thought such traps would work for an electric dipole measurement on electrons. These measurements require that we expose our molecules to electric fields, and if the molecules are charged ions, the electric fields should cause them to accelerate away. But the head of our lab, Eric Cornell, had an exciting insight: he suggested that we rotate the electric field fast enough that, instead of flying away, the ions just trace out small circles within the trap. This method let us measure our molecules for three seconds—a great improvement on previous experiments. Our measurement time was limited mainly by the time it took for our molecules to decay into lower-energy states.
Our ion trap technique does have a drawback, though. Because we could trap only so many ions at once, our experiment measured many fewer electrons in each run than typical beam experiments. We were able to observe a few hundred electrons per shot. Over two months of long days in the lab, we measured more than 100 million electrons in total.
Gathering the data set was the quick part. The real challenge of a precision experiment is the time spent looking for systematic errors—ways we might convince ourselves we had measured an eEDM when in fact we had not. Precision-measurement scientists take this job very seriously; no one wants to declare they have discovered new particles only to later find out they had only precisely measured a tiny flaw in their apparatus or method. We spent about two years hunting for and understanding such flaws.
An important source of errors in EDM experiments is the level of control over the magnetic field. Recall that we are looking for a difference in the wobble frequency of an electron in a magnetic field when an electric field is applied parallel to and then opposing the direction of that magnetic field. The problem is that the wobble frequency depends on the strength of the magnetic field. If that field drifts slightly between the two measurements, the result will look like an EDM. To address this possibility, we found a way to do both electric field measurements simultaneously. We take a cloud of molecules and prepare half with their internal electric field aligned with the external magnetic field and half with their internal electric field antialigned. We then measure the wobbles of electrons in both groups simultaneously, and because both are in the same trap at the same time, they experience the same magnetic fields to very high precision.
Another source of systematic error is experimenter bias. All scientists are human beings and, despite our best efforts, can be biased in our thoughts and decisions. This fallibility can potentially affect the results of experiments. In the past it has caused researchers to subconsciously try to match the results of previous experiments. A well-studied example is in measurements of the speed of light. In the late 19th century attempts to determine this constant overestimated it significantly. Later, measurements tended to underestimate the value, leading some physicists to suggest that the speed of light was changing. But in fact, researchers were probably unconsciously steering their data to fit better with previous values, even though those turned out to be inaccurate. It wasn’t until experimenters had a much better grasp on the true size of their errors that the various measurements converged on what we now think is the correct value.
To avoid this issue, many modern precision-measurement experiments take data “blinded.” In our case, after each run of the experiment, we programmed our computer to add a randomly generated number—the “blind”—to our measurements and store it in an encrypted file. Only after we had gathered all our data, finished our statistical analysis and even mostly written the paper did we have the computer subtract the blind to reveal our true result.
The day of the unveiling was a nerve-racking one. After years of hard work, our team gathered to find out the final result together. I had written a computer program to generate a bingo-style card with 64 plausible numbers, only one of which was the true result. The other numbers varied from “consistent with zero” to “a very significant discovery.” Slowly, all the fake answers disappeared from the screen one by one. It’s a bit weird to have years of your professional life condensed into a single number, and I questioned the wisdom of amping up the stress with the bingo card. But I think it became apparent to all of us how important the blinding technique was; it was hard to know whether to be relieved or disappointed by the vanishing of a particularly large result that would have hinted at new, undiscovered particles and fields but also contradicted the results of previous experiments.
Finally, a single value remained on the screen. Our answer was consistent with zero within our calculated uncertainty. The result was also consistent with previous measurements, building confidence in them as a collective, and it improved on the best precision by a factor of two. So far, it seems, we have no evidence that the electron has an EDM.
Though perhaps not as exciting as a nonzero value, our new upper limit on the possible size of the eEDM has substantial consequences. If we assume that any new CP-violating field couples to electrons with a strength similar to that of the electromagnetic field (a middling coupling strength in the Standard Model, between those of the fields representing the weak and strong forces), our measurement means that the mass of its associated particle must be more than roughly 40 tera electron volts. This limit would place it far beyond the highest mass of a particle that could be directly discovered at the LHC.
This result, and those of other recent eEDM measurements, is surprising to many who expected new fields to exist below this energy scale. One possible explanation is that the fields couple to the Standard Model in such a way that their contribution to the eEDM is only indirect and therefore smaller for a given mass than the estimate above assumes. Researchers might be able to confirm this possibility by making complementary measurements of EDMs in other particles built from quarks where the coupling is likely to be different. Such measurements are currently underway for neutrons and for mercury nuclei, and many more are planned.
Another possibility is that the new fields are at just slightly higher energies or smaller couplings, out of reach of our experiment but accessible to the next generation of eEDM measurements. I expect the next decade or so to see significant precision improvements. At JILA, we’re already working on using a different molecule, thorium fluoride, which has a stronger internal electric field, to increase the observation time still further, perhaps out to 20 seconds. We’re also planning to partially address our disadvantage in the number of molecules we can trap by running many copies of the experiment in parallel with tens of separate traps in one long vacuum chamber.
And we expect to see major advances from the latest iteration of the world’s best molecular beam experiment, the ACME III project (for “advanced cold molecule EDM”), based at Northwestern University, where scientists are improving the focus of their molecular beam to extend their measurement time. Simultaneously, other physicists are working on ways to trap neutral molecules using laser-cooling techniques. This method could potentially combine the advantages of long measurement times and large numbers of electrons. And an ambitious plan by researchers in Canada aims to study molecules confined inside a solid crystal of frozen noble gas. This technique could enable measurements of colossal numbers of electrons in each shot, but it remains to be seen how the fields from other nearby atoms in the solid will affect the measurement.
Ultimately, we hope to either detect an electric dipole moment in an electron or limit its possible size enough to effectively rule out the types of fields and particles scientists have envisioned to explain our antimatter mystery. We know there must be some reason out there for the universe of matter we live in to be the way it is—the question is how long it will take us to discover it.
Source link